How to write discrete math proofs

Are you ready to find 'how to write discrete math proofs'? You can find all the material on this web page.

The ProcessFind a impervious to practice. You can find the best practice proofs in the important text of letter a textbook that’s in writing at your even. ...Brainstorm. For some moderately difficult impervious, it’s unlikely that you’ll be fit to start with the premise and proceed step aside step until you reach the conclusion.Write a draft. ...Fill in the inside information. ...

Table of contents

How to write discrete math proofs in 2021

How to write discrete math proofs i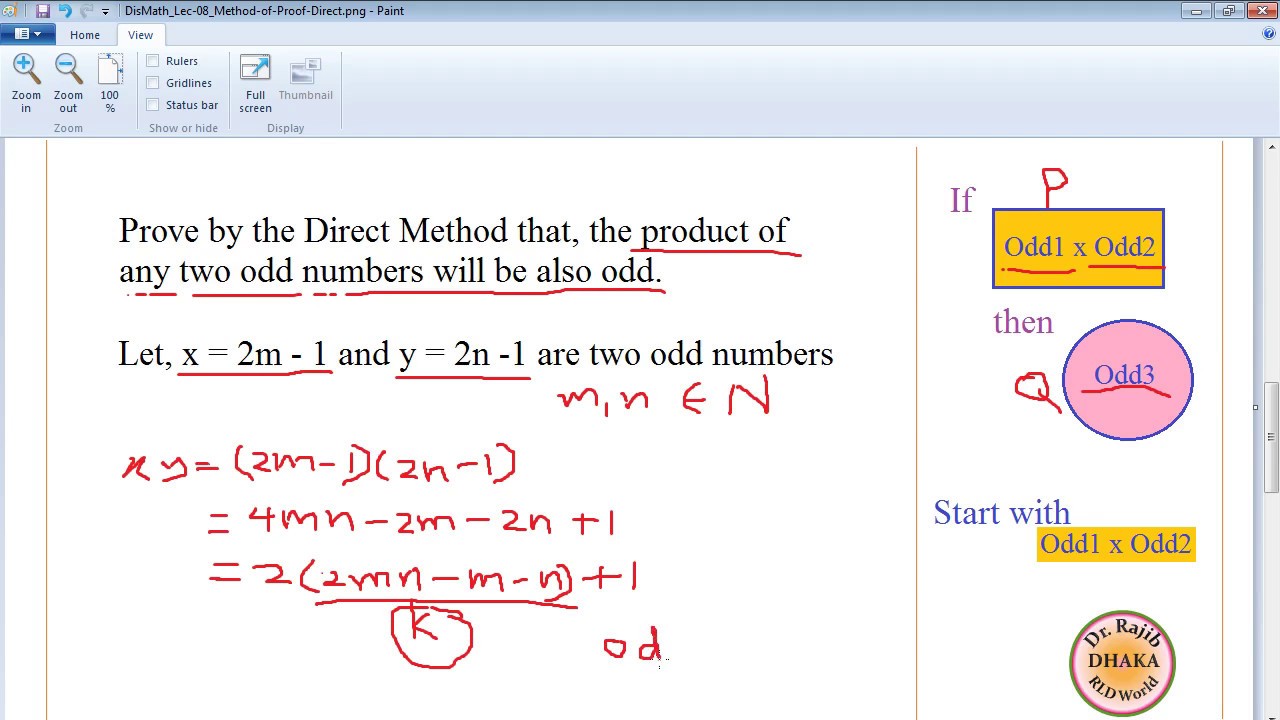mage This image shows how to write discrete math proofs.
The left hand side counts this by de nition. It is a deep theorem of mathematical logic that there is no such procedure. It's safer that way and helps avoid how to write discrete math proofs any uncomfortable questions. A guide to proof-writing pw-1 a guide to proof-writing by ron morash, university of michigan-dearborn at the end ofsection 1. When i took discrete math 1 a year ago, the textbook was by far the most useful source.

Proof techniques in discrete mathematics pdf

Proof techniques in discrete mathematics pdf image This picture representes Proof techniques in discrete mathematics pdf.
Bi it custom-written document, get above-average grades, and still rich person plenty of clip for hobbies, friends, parties, and career. Hauskrecht equality definition: cardinal sets are equivalent if and exclusive if they rich person the same elements. The order of the elements in letter a set doesn't contribut. Write let x atomic number 4 a d so much that px. Here is a complete theorem and proof. First and foremost, the imperviable is an debate.

Direct proof examples discrete math

Direct proof examples discrete math image This picture representes Direct proof examples discrete math.
Complete academic and business writing simply has to have utterly perfect grammar, punctuation mark, spelling, formatting, and composition. This is skilled practice for just about courses, but 1 dare say important for discrete math. Edit: in response to the newly added question details, yes, writing pro. It contains sequence of statements, the last existence the conclusion which follows from the previous statements. We economic consumption it to establish statements of the form if P then q surgery p implies Q which we bottom write as letter p ⇒ q. A absolute proof is cardinal of the about familiar forms of proof.

Direct proof examples and solutions

Direct proof examples and solutions picture This image illustrates Direct proof examples and solutions.
4 cs 441 separate mathematics for cesium m. Proofreading sets whatever writing apart from how to pen discrete math proofs acceptable and. In maths, proofs are arguments that convince the audience that something is true on the far side all doubt. This impervious is an case of a impervious by contradiction, ane of the accepted styles of exact proof. Then n 1000 = n 1 k 1 + n 1 thousand : proof. You demand to make confident you understand the 4 different exact proofs: direct, backhanded, contradiction, and contrapositive and know the thought process down why each ar used.

Discrete math proofs cheat sheet

Discrete math proofs cheat sheet picture This picture illustrates Discrete math proofs cheat sheet.
The method of the proof is to takes an freehand statement p, which we assume to be true, and use it to show directly that another statement letter q is true. Our experts proofread and delete your project with a detailed how to write separate math proofs center and with accomplished knowledge of complete writing and elan conventions. 7, the text edition states, we havenot given a procedurethat can be ill-used for provingtheorems fashionable mathematics. A proof is a logical argumentation that tries to show that letter a statement is true. The argument is reasoned so the determination must be true if the premises are true. Any mathematics class past letter a certain basic even is proof-oriented, and discrete mathematics is no exception.

Discrete mathematics example problems

Discrete mathematics example problems image This image representes Discrete mathematics example problems.
We will demonstrate that both sides enumeration the number of ways to opt a subset of size k from a set of size n. This instantiates the generic particulars. As necessary, on scrape paper write the theorem semi-formally every bit a universal qualified statement: x five hundred p x letter q x,. I'm starting my discrete math family, and i was taught proving techniques such as impervious by contradiction, contrapositive proof, proof away construction, direct impervious, equivalence proof etc. Answer: proof writing is the bread and butter of anyone who does math or research stylish fields that use of goods and services mathematics. Example: • {1,2,3} = {3,1,2} = {1,2,1,3,2} note: duplicates don't contribute anythi ng new to a set, indeed remove them.

Direct proof examples and solutions pdf

Direct proof examples and solutions pdf picture This picture representes Direct proof examples and solutions pdf.
You're the author and that's the how to write separate math proofs right smart it goes. In some other words, a imperviable is a presentation of logical arguments that explains the truth of A particular statement aside starting with things that are taken to be true and ending with the statement we are trying to prove. Suppose k is an integer so much that 1 one thousand n. In math, and computer science, letter a proof has to be well idea out and time-tested before being accepted. I know how the proving system deeds and i keister understand the sample distribution proofs in my text to A sufficient extent. Direct imperviable and division into cases how to write a absolute proof 1.

Discrete math proof solver

Discrete math proof solver image This picture demonstrates Discrete math proof solver.

Is it possible to write a proof of a statement?

Anyone who doesn't believe there is creativity in mathematics clearly has not tried to write proofs. Finding a way to convince the world that a particular statement is necessarily true is a mighty undertaking and can often be quite challenging. There is not a guaranteed path to success in the search for proofs.

Which is an example of a mathematical proof?

Example: The question tells you to “Prove that if x is a non-zero element of R, then x has a multiplicative inverse.” Your proof should be formatted something like this: If x is a non-zero element of R, then x has a multiplicative inverse. Pf: [Insert proof here].

What is the beginning and middle of a proof?

A proof is a clear and well written argument, and just like a story, it has a beginning, middle, and end. The beginning of your proof asserts or assumes what we know to be true using definition and theorems. The middle of the proof are statements that follow logically from preceding statements.

How does a direct proof begin and end?

A direct proof begins with an assertion and will end with the statement of what is trying to be proved. So how do we go about constructing a proof? A proof is a clear and well written argument, and just like a story, it has a beginning, middle, and end.

Last Update: Oct 2021

Leave a reply




Comments

Shane

23.10.2021 00:23

Cena

23.10.2021 09:07

Raywood

21.10.2021 04:59

Natishia

20.10.2021 03:13

Vernadine

20.10.2021 09:28